PHP 二叉树 类实现

该类 仅实现普通的二叉树

// 安装使用如下 git clone git@github.com:wschat/tree.git cd tree composer dump-autoload Demo 演示 Node 类演示代码testNode.php Tree sort辅助排序类演示代码testSort.php Tree insert插入操作方法演示代码testTreeInsert.php Tree tree()、left()、end()、closest()、树生成方法演示代码testTree.php Tree init()方法使用 多项插入方法演示代码testTreeLimit.php Tree 统计、遍历方法演示代码testTreeOrder.php

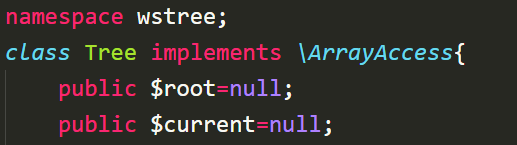
文档完善 （注：Node、Tree 均实现了ArrayAccess接口）

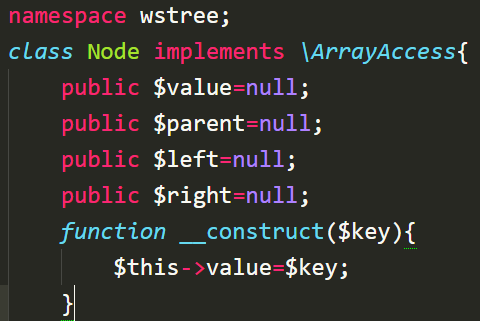
A / B C （图2） / D E / / G H F

init($array,$options=[],$parent=null) 快速的生成一个二叉树（图2）为例

* array $array 用户数据 * array $options 额外参数 [$pid=0,$sort=true,$pidKey='pid',$level=0]; * integer $pid 起始pid值 * boolean $sort 是否先进行按主键值的排序 * string $pidKey 指向父级的键名 * integer $level 级别默认为0 $array每一项均注入一个字段_level起始值为$level+1 如图2：A:1 D:3

$data=[ ['id'=>1,'name'=>'A','pid'=>0], ['id'=>2,'name'=>'B','pid'=>1], ['id'=>3,'name'=>'C','pid'=>1], ['id'=>4,'name'=>'D','pid'=>3], ['id'=>5,'name'=>'E','pid'=>3], ['id'=>6,'name'=>'F','pid'=>5], ['id'=>7,'name'=>'G','pid'=>4], ['id'=>8,'name'=>'H','pid'=>4], ]; shuffle($data); // 这只是打乱数组 $tree=new wstreeTree(); $tree->init($data); print_r($tree['root']); // print_r($tree->root);

如果想更灵活的组合二叉树 tree($key)、leaf(key)、end()、closest($childNums=2)、可以帮到你（根节点：Tree::$root、指针：Tree::$current）

* tree($key) 将$node=new Node($key)插入树中(从左到右)，指针指向(当前)$node，如果树没有根节点则第一个插入的Node实例设为根节点 * leaf($key) 将$node=new Node($key)插入树中(从左到右)，指针指向(上级)$node->parent，如果树没有根节点则直接执行tree($key) * end() * closest($childNums=2) 将指针指向最近的可插入节点的节点（如果均不满足则返回根节点）当然你也可以多次使用end()方法代替 $childNums 默认为2 可选1、2 。（如果你想使用其它也不影响使用）

A / B C （图3） / / I J D E / / / / k L M N G H F 如（图3）我们实现一个更复杂的实例

$tree ->tree('A') ->tree('B') ->tree('I') ->leaf('K') ->leaf('L') ->end() ->tree('J') ->leaf('M') ->leaf('N') ->closest(2) //这里使用了 closest() 将指针指向了A（因为上述每一个节点都有了2个子集） ->tree('C') //如果你觉得有点乱 其实到这一步 我们已经使用了所有的方法 ->tree('D') ->leaf('G') ->leaf('H') ->end() ->tree('E') ->leaf('F'); print_r($tree['root']);

preOrder($node,$callback) 先序遍历

* Node $node 一个节点(当然这个节点必须存在于Tree中) * function $callback 回调函数(允许匿名) 参数为遍历的节点

// 这是一个扩展的功能 $count => 8 $count=null; // $tree 来源（图2） $tree->preOrder($tree['root'],function($item)use(&$count){ echo $item['value']['name']; $count++; }); // 输出：ABCDGHEF

inOrder($node,$callback) 中序遍历

* Node $node 一个节点(当然这个节点必须存在于Tree中) * function $callback 回调函数(允许匿名) 参数为遍历的节点

// $tree 来源（图2） $tree->inOrder($tree['root'],function($item){ echo $item['value']['name']; }); // 输出：BAGDHCFE

postOrder($node,$callback) 后序遍历

* Node $node 一个节点(当然这个节点必须存在于Tree中) * function $callback 回调函数(允许匿名) 参数为遍历的节点

// $tree 来源（图2） $tree->postOrder($tree['root'],function($item){ echo $item['value']['name']; }); // 输出：ABCDGHEF

levelOrder($node,$callback) 层层遍历

* Node $node 一个节点(当然这个节点必须存在于Tree中) * function $callback 回调函数(允许匿名) 参数为遍历的节点 * $callback的参数与另三个遍历参数有区别(会返回空节点 null )

// $tree 来源（图2） $tree->levelOrder($tree['root'],function($item){ echo '<br>'.$item['value']['name']; }); // 输出： A B C null null D E G H F null null null null null

boolean isFull($node=null) 是否满二叉树

* $node 默认为根节点

// $tree 来源（图2） echo $tree->isFull($tree->root); //$tree->isFull();

boolean isComplete($node=null) 是否完全二叉树

* $node 默认为根节点

// $tree 来源（图2） echo $tree->isComplete($tree->root); //$tree->isComplete();

integer getDepth($node) 获取当前节点深度 根节点深度为 1

* $node 节点

// $tree 来源（图2） echo $tree->getDepth($tree->root); // 1;

integer getHeight($node) 获取当前节点高度(最大高度) 叶节点高度为 1

* $node 节点

// $tree 来源（图2） echo $tree->getHeight($tree->root); // 4;

integer getMinHeight($node) 获取当前节点高度(最小高度) 叶节点高度为 1

* $node 节点

// $tree 来源（图2） echo $tree->getMinHeight($tree->root); // 2;

以下是关于两个insert方法在特定情况下的使用 （落位弱区 如（图4）是一个在A下插入子节点的操作）

A A A A / / / / B C => B C => B C => B C （图4） / / / / / / / D D E D F E D F E G

insertable($node,$natural=false) 查询可插入的节点信息(公排 | 弱区落位)

* $node 需要在该节点下插入 不一定是根节点 $node必须存在于树中 * $natural false：弱区落位 true：公排（从上到下做到右 类似levelOrder()）

// $tree 来源（图2） $parent=$tree->insertable($tree['root']); // B $parent=$tree->insertable($tree['root']['left']); // B $parent=$tree->insertable($tree['root']['right']); // E

insert($key,$node=null,$natural=false) 插入新节点(公排 | 弱区落位)

* $key 需要插入的值 * $node 需要在该节点下插入 不一定是根节点 $node必须存在于树中 * $natural false：弱区落位 true：公排（从上到下做到右 类似levelOrder()） * 返回新增的节点，这只是在insertable()方法的基础上进行自我判断并插入操作

// $tree 来源（图2） $result=$tree->insert('I',$tree['root']);

两个扩展方法 childrens()、 preSort()、

childrens($array,$pidKey='pid') 子集个数统计（直属下级），注入每一项_childrens字段(init() 中使用到)

* array $array 一个有特定规律的二维数组 * string $pidKey 指向父级的键名

// 注：以下两个方法均以该数据为例 $data=[ ['id'=>1,'name'=>'A','pid'=>0], ['id'=>2,'name'=>'B','pid'=>1], ['id'=>3,'name'=>'C','pid'=>1], ['id'=>4,'name'=>'D','pid'=>3], ['id'=>5,'name'=>'E','pid'=>3], ['id'=>6,'name'=>'F','pid'=>5], ['id'=>7,'name'=>'G','pid'=>4], ['id'=>8,'name'=>'H','pid'=>4], ]; $result=Tree::childrens($data,'pid');

preSort($array,$pidKey='pid') 先序 排序 以及是否存在子集判断（增加_level字段 深度 0 起始。 getDepth()方法为 1 起始）

* array $array 一个有特定规律的二维数组 * string $pidKey 指向父级的键名

shuffle($data); $result=Tree::_childrens($data,'pid'); // _prefix 以_level基准填充8倍的