"一阶滤波_200 Smart" 这个术语可能指的是一种特定的滤波器设计或应用,结合了“一阶滤波”和“200 Smart”这两个概念。以下是对这两个部分的解释:
1. "一阶滤波":在信号处理和控制系统领域中,一阶滤波器是一种简单的滤波器,它由一个电阻和一个电容(RC)组成,或者在一个数字信号处理中由一个简单的差分方程表示。一阶滤波器可以用来降低信号中的噪声或平滑信号,但它对频率变化的响应相对较慢。
2. "200 Smart":这部分可能指的是某种特定的型号、规格或特性。例如,它可能指的是一个具有200个智能特性或功能的设备、系统或软件。具体是哪些特性或功能,需要更多的上下文信息来解释。
如果“一阶滤波_200 Smart”是指一个具体的滤波器设计或产品,那么它可能是一种具有200个智能特性的、基于一阶滤波原理的设备或系统。这种设备或系统可能具有自动调整滤波参数、自适应噪声抑制、智能信号处理等功能,以提高信号质量或系统性能。
然而,由于缺乏具体的上下文信息,以上解释仅供参考。如果需要更准确的解释,请提供更多的信息或详细描述。
相关内容:
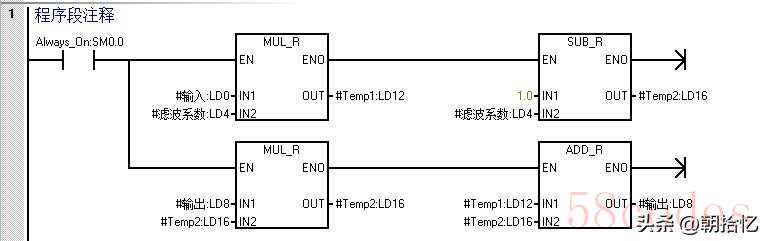
一阶滤波,又叫一阶低通滤波,是一个能够过滤掉高频信号使数据变平滑的算法。公式为:Y(n)=k*X(n) +(1-k)*Y(n-1)即:本次输出值 = 滤波系数 x 本次采样值 +(1 - 滤波系数)x 上次输出值本次输出值是本次采样值和上次输出值的加权求和,且权重和为1。滤波系数k取值0-1,k越大,本次采样值的权重越大,本次输出值对本次采样值的变化就越灵敏。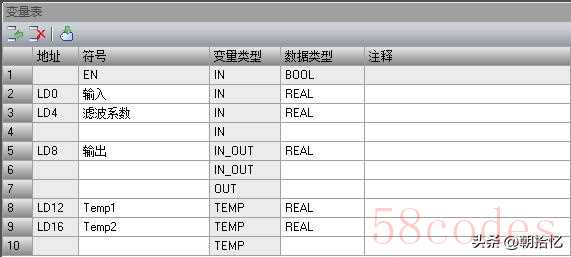
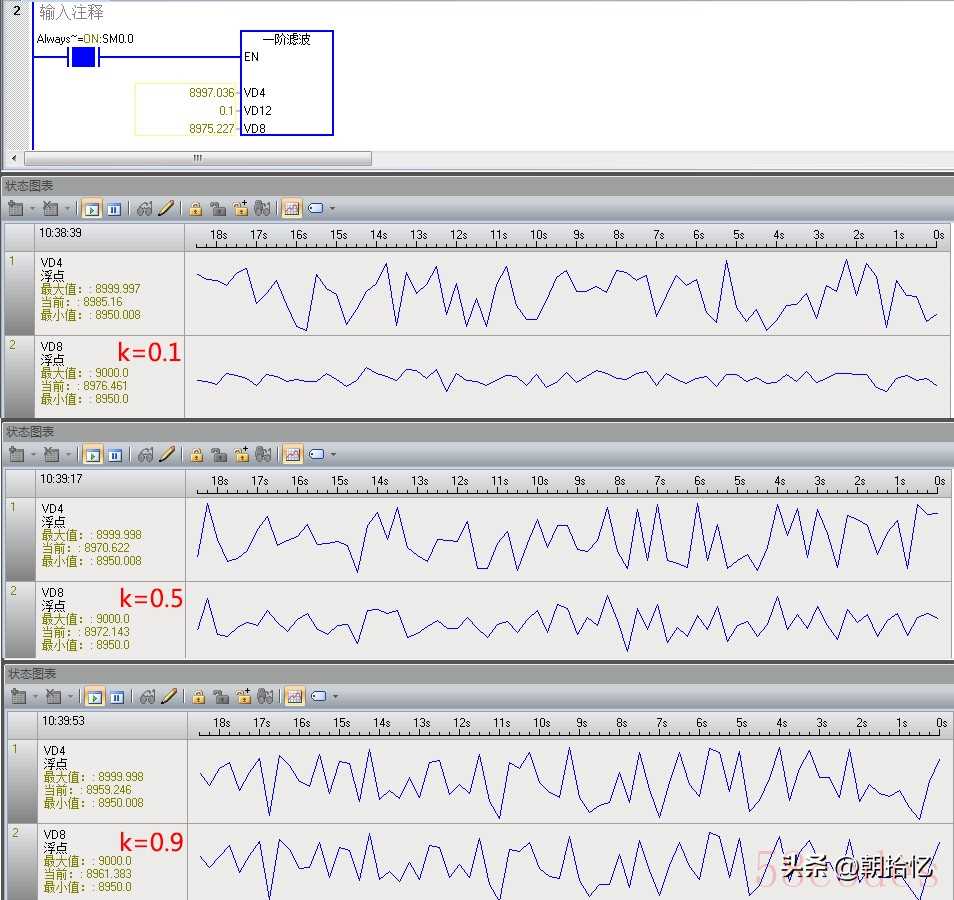 可以看出,k值越大,滤波结果灵敏度越高,越不稳定。当然,以上只是对数据稳定波动情况下的分析,不具普遍性。
可以看出,k值越大,滤波结果灵敏度越高,越不稳定。当然,以上只是对数据稳定波动情况下的分析,不具普遍性。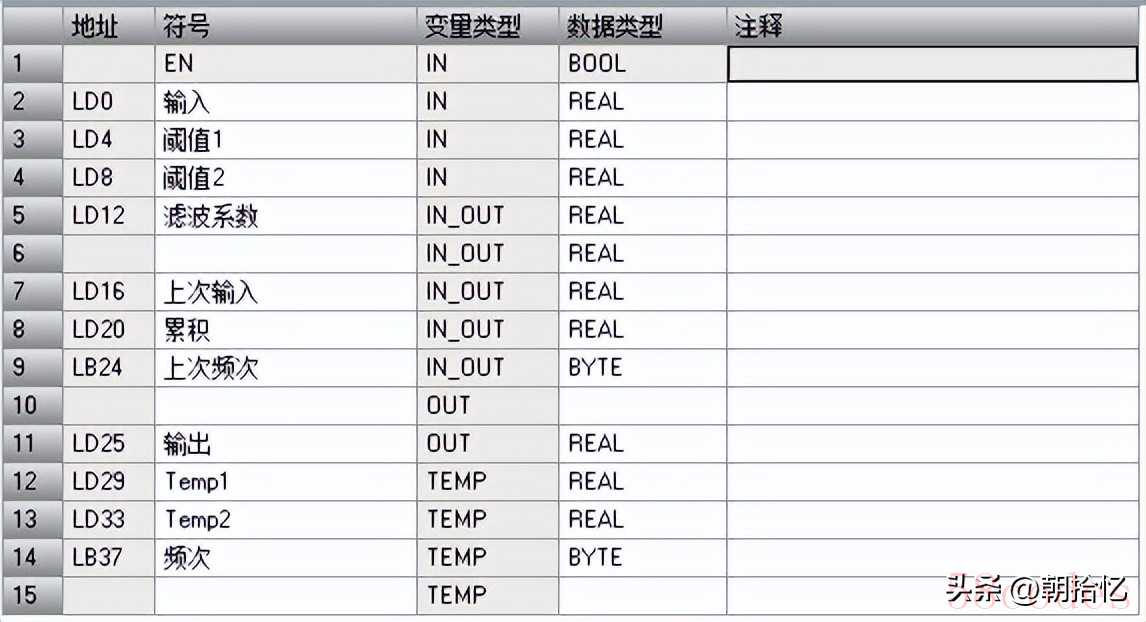
基本程序:


不同k值的滤波结果:
 可以看出,k值越大,滤波结果灵敏度越高,越不稳定。当然,以上只是对数据稳定波动情况下的分析,不具普遍性。
可以看出,k值越大,滤波结果灵敏度越高,越不稳定。当然,以上只是对数据稳定波动情况下的分析,不具普遍性。实际应用:
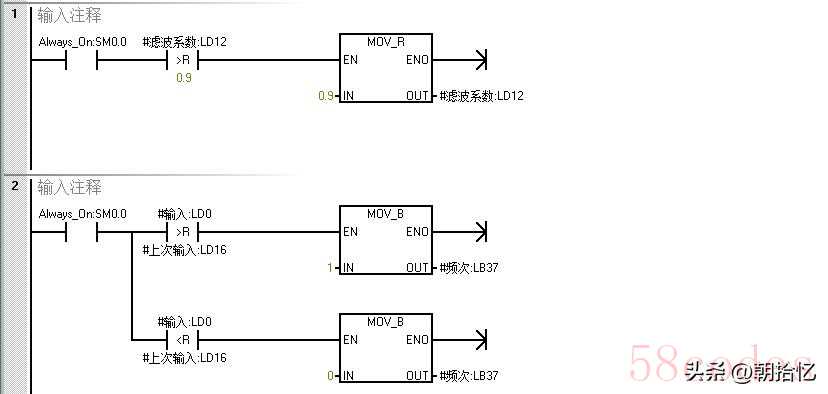
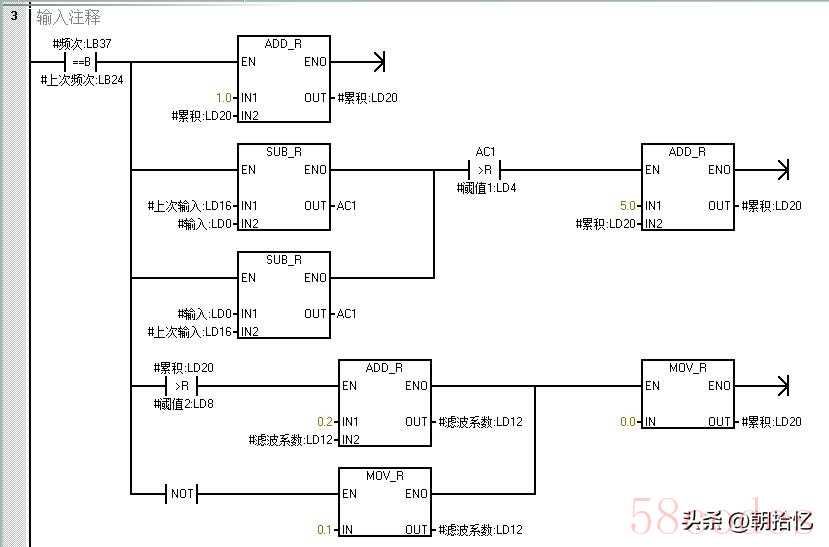
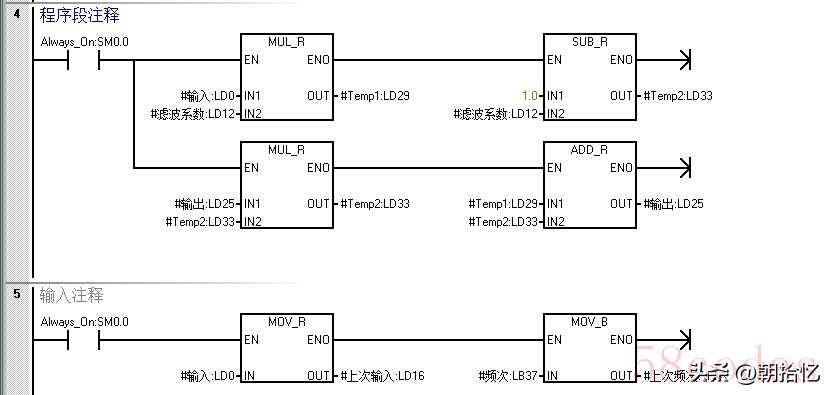
实际使用中,对于不同的数据变化趋势,需要取不同的滤波系数:● 数据有偶然干扰时,k值取0,忽略干扰期间的采样值;● 数据稳定波动时,k值取小,减小波动的权重,使滤波结果平滑稳定;● 数据持续的真实地变化时,一方面,滤波结果要迅速趋近于新采样数据,且数据变化越快,趋近速度越快;另一方面,数据重新稳定时,滤波结果要迅速趋于稳定。应用到程序中,主要就是判断采样数据是否持续地增加或减少:是的话,累计该持续性变化的频次,当该频次超过设定的阈值,加大滤波系数并重新累计该频次(特别地,当变化幅度超过设定的阈值1,加快频次的累计);否的话,设小滤波系数并复位频次。变滤波系数的程序如下(未测试,水平有限仅供参考):

滤波系数限幅,采样数据增减判定

滤波系数计算

滤波输出计算,参数回传
相关资料:【滤波器学习笔记】一阶RC低通滤波_Jim勉的博客-CSDN博客_一阶rc滤波
 微信扫一扫打赏
微信扫一扫打赏
 支付宝扫一扫打赏
支付宝扫一扫打赏
